
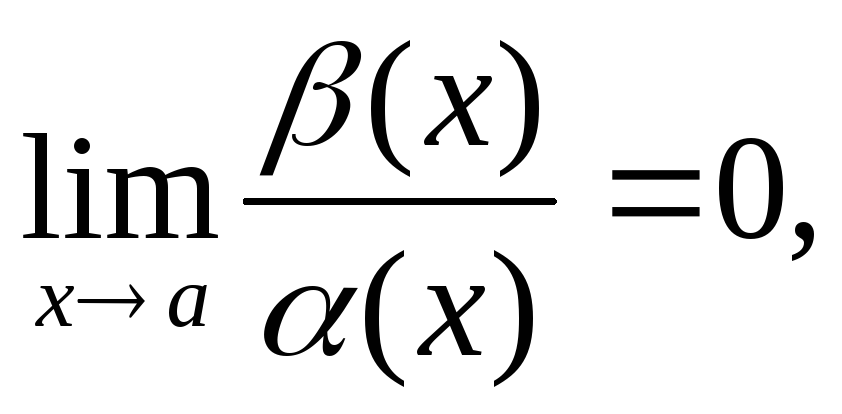
Note that, generally, books (such as Keisler's Elementary Calculus: An Infinitesimal Approach) that approach Calculus from the perspective of infinitesimals also discuss epsilon-delta limits the concept is so standard that it's hard to learn calculus without encountering it. By an infinitesimal they mean any function that has limit at. The primary reason epsilon-delta limits were introduced and standardized was that infinitesimals were unable to be made rigorous. Some people like to make up a story about replacement in such limits using special terminology. However, they are generally much more rarely encountered today. Both Leibniz and Newton thought in terms of them.
Limits and infinitesimals series#
A series of important concepts in mathematical analysis, such as the continuity of the function, the derivative (. Infinitesimals seem more intuitive to me - although I have not looked into them extensively, I often think of things as infinitesimals first and then translate my thoughts to limits. Epsilon-delta limits are by far the most popular approach and are how the subject is most often taught. Infinitesimals seem more intuitive to me - although I have not looked into them extensively, I often think of things as infinitesimals first and then translate my thoughts to limits. The limit idea is the basic idea of calculus. There is rarely a simple 'better' for this sort of thing. There is rarely a simple "better" for this sort of thing.Įpsilon-delta limits are by far the most popular approach and are how the subject is most often taught.


 0 kommentar(er)
0 kommentar(er)
